GPCA is an algebraic subspace clustering technique based on polynomial fitting and differentiation. The key idea is to represent the number of subspaces as the degree of a polynomial and encode the subspace bases as factors of these polynomials.

For the sake of simplicity, assume that the data was distributed on a collection of two hyperplanes, each of one can be represented by the equation x^Tb_i=0. By multiplying the two equations for the two subspaces, we obtain

where p(x) is a homogeneous polynomial of degree two in the coordinates of x which is satisfied by all data points, regardless of which hyperplane they belong to. Therefore this polynomial can be considered as a global model representing all subspaces.

As with any polynomial, p(x) may be expanded linearly in terms of some coefficients with respect to a basis of polynomials. Therefore, given enough data points from the subspaces, the coefficients of p(x) can be linearly estimated from the data by using a non-linear embedding (the Veronese map). Building upon our previous example, assume that x lives in R³, say x=[x,y,z]^T. Then, p(x) can be expanded as

It is immediate to note that the polynomial is non-linear in the coordinates x,y,z but is linear in the coefficients a,b,c,d,e,f. The latter can be therefore retrived (up to a scale factor) by solving the homogeneous linear system

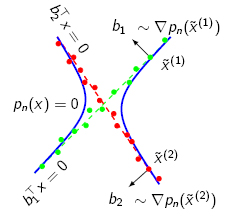
Now, the set of points x such that p(x)=0 can be thought of as a surface (in our previous example, p(x) is the equation of a conic in the projective plane P²). Moreover, the gradient of p(x), ∇p(x) must be orthogonal to this surface. Since the surface is a union of subspaces, the gradient at a point must be orthogonal to the subspace passing through that point. As a result, we may compute the normal vectors at a point as the gradient of p(x) at that point, as illustrated in the figure below.

Since all points in the same cluster should have the same (or similar) normal vectors, we can cluster the data by clustering these normal vectors. In fact, the angles between these normal vectors provide use with a similarity measure that can be used together with spectral clustering.

In the case of hyperplanes, a single polynomial is enough, but in the case of subspaces of different dimensions, it is necessary to fit more polynomials. The gradient of each one of these polynomials at a point x will give possibly a different normal vector. All these normal vectors will form a basis for the complement of the subspace passing through x. The principal angles between these orthogonal subspaces may now be used to define a similarity measure, and clustering proceeds as before. More details can be found in the references.

GPCA is an algebraic technique which provide the exact algebraic solution in closed form when the data is perfect. With a moderate amount of noise, GPCA will still operate correctly, as the polynomials can be estimated using least squares. However, in the presence of large amounts of noise and outliers, the coefficients may be estimated incorrectly. For this reason, some variations of the main algorithm have been developed. Some of these employ spectral clustering, voting schemes, multivariate-trimming and influence functions to deal with non-perfect data. Please refer to the page from UIUC for more details and code samples on this topic.

An implementation of GPCA in Matlab (with applications to motion segmentation) is also available from our group. See the Code page.

GPCA has been successfully applied in various field of computer vision. In the following we present a (non-exaustive) list of applications that are based on the ideas of GPCA. Please refer to the specific webpages on this same website for more details on this topic.