 In 1948 Shanon laid the foundations of information theory which revolutionized
statistics, physics, engineering, and computer science. A strong limitation,
however, is that the semantic content of data is not taken into account. This
research will produce a novel framework for characterizing semantic
information content in multimodal data. It will combine non-convex
optimization with advanced statistical methods, leading to new representation
learning algorithms, measures of uncertainty, and sampling methods. Given
data from a scene, the algorithms will be able find the most informative
representations of the data for a specific task. These methods will be
applied to complex datasets from real situations, including text, images,
videos, sensor signals, and cameras, resulting in intelligent decision based
algorithms.
In 1948 Shanon laid the foundations of information theory which revolutionized
statistics, physics, engineering, and computer science. A strong limitation,
however, is that the semantic content of data is not taken into account. This
research will produce a novel framework for characterizing semantic
information content in multimodal data. It will combine non-convex
optimization with advanced statistical methods, leading to new representation
learning algorithms, measures of uncertainty, and sampling methods. Given
data from a scene, the algorithms will be able find the most informative
representations of the data for a specific task. These methods will be
applied to complex datasets from real situations, including text, images,
videos, sensor signals, and cameras, resulting in intelligent decision based
algorithms.
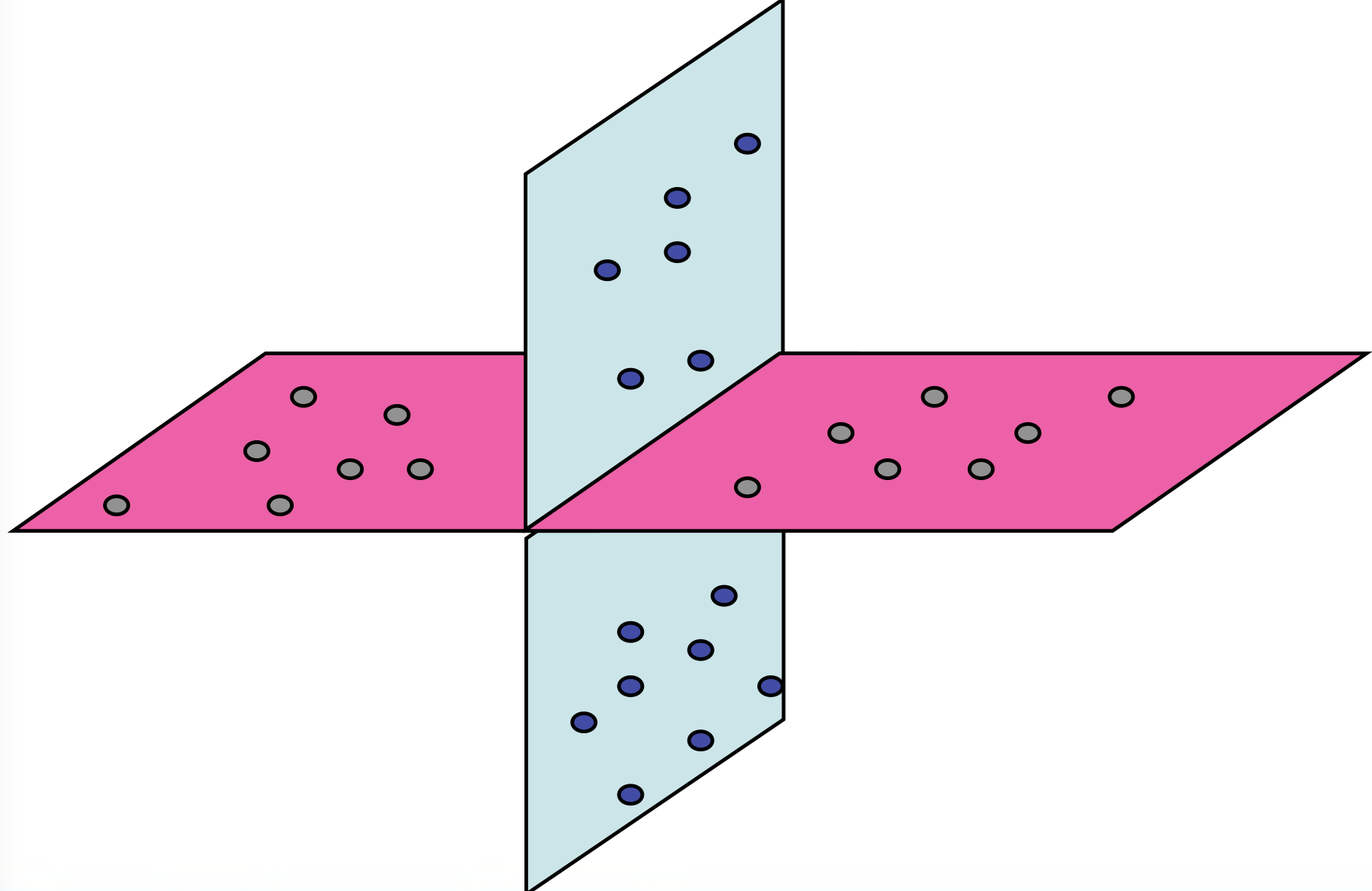 Existing theory and algorithms for discovering structure in high-dimensional data rely on the assumption that the data can be well approximated by low-dimensional structures.
This project will develop provably correct and scalable optimization algorithms for learning a union of high-dimensional subspaces from big and corrupted data. The proposed algorithms will be based on a novel framework called Dual Principal Component Pursuit that, instead of learning a basis for each subspace, seeks to learn a basis for their orthogonal complements by solving a family of non-convex sparse representation problems. We develop scalable algorithms for solving these non-convex optimization problems and study conditions for their convergence to the global optimum. Applications of these methods include segmentation of point clouds and clustering of image categorization datasets.
Existing theory and algorithms for discovering structure in high-dimensional data rely on the assumption that the data can be well approximated by low-dimensional structures.
This project will develop provably correct and scalable optimization algorithms for learning a union of high-dimensional subspaces from big and corrupted data. The proposed algorithms will be based on a novel framework called Dual Principal Component Pursuit that, instead of learning a basis for each subspace, seeks to learn a basis for their orthogonal complements by solving a family of non-convex sparse representation problems. We develop scalable algorithms for solving these non-convex optimization problems and study conditions for their convergence to the global optimum. Applications of these methods include segmentation of point clouds and clustering of image categorization datasets.
 Existing methods for processing images generally succeed only when the data are
balanced and homogeneous. This project develops a new recognition framework
based on novel sparse and low-rank modeling techniques to overcome these
limitations. Imbalanced data are automatically divided into common and rare
patterns, so that a small set of balanced representatives can be selected. To
capture information across multiple domains and modalities, we use non-convex
methods to learn shared latent representations. Classification and clustering
algorithms can then be applied to the latent representation. Applications of
these methods include image and video-based object recognition, activity
recognition, video summarization, and surveillance.
Existing methods for processing images generally succeed only when the data are
balanced and homogeneous. This project develops a new recognition framework
based on novel sparse and low-rank modeling techniques to overcome these
limitations. Imbalanced data are automatically divided into common and rare
patterns, so that a small set of balanced representatives can be selected. To
capture information across multiple domains and modalities, we use non-convex
methods to learn shared latent representations. Classification and clustering
algorithms can then be applied to the latent representation. Applications of
these methods include image and video-based object recognition, activity
recognition, video summarization, and surveillance.
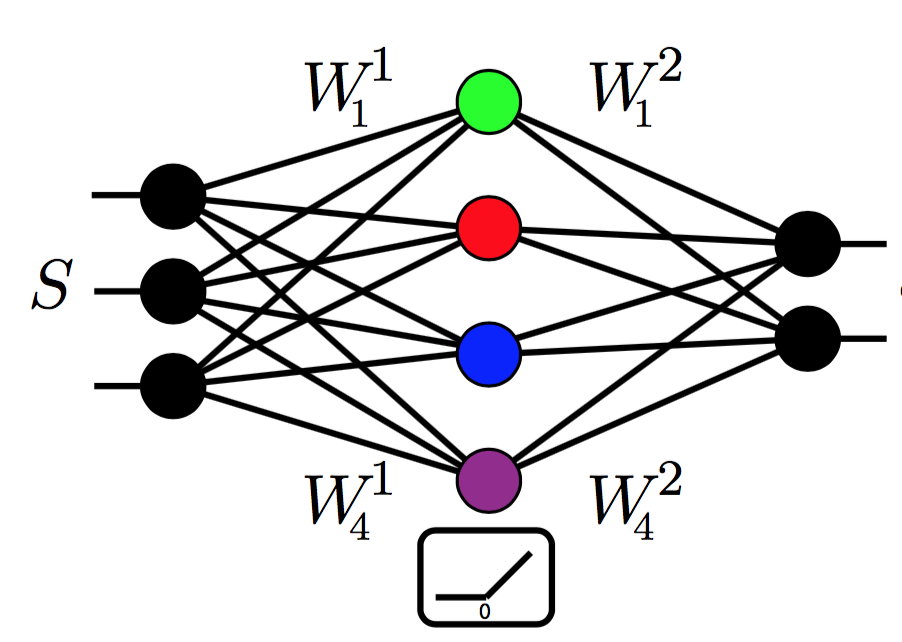 This project seeks to develop a mathematical framework for the analysis of a
broad class of non-convex optimization problems, including matrix
factorization, tensor factorization, and deep learning. In particular, this
project focuses on the problem of minimizing the sum of a loss function and a
regularization function, both of which can be non-convex. Specific goals
include characterizing conditions on the loss function, the product map, the
network architecture and the regularization strategy that give guarantees of
global optimality, provide theoretical insights for the success of existing
optimization algorithms and architectures, and offer guidance in the design of
novel network architectures.
This project seeks to develop a mathematical framework for the analysis of a
broad class of non-convex optimization problems, including matrix
factorization, tensor factorization, and deep learning. In particular, this
project focuses on the problem of minimizing the sum of a loss function and a
regularization function, both of which can be non-convex. Specific goals
include characterizing conditions on the loss function, the product map, the
network architecture and the regularization strategy that give guarantees of
global optimality, provide theoretical insights for the success of existing
optimization algorithms and architectures, and offer guidance in the design of
novel network architectures.
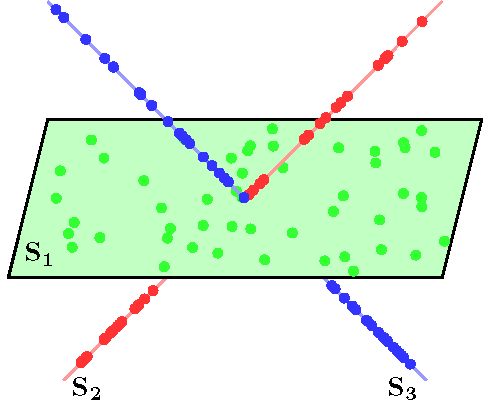 Sparse subspace clustering (SSC) is a method for clustering high-dimensional data
living in a union of low-dimensional subspaces. SSC uses the sparse representation of
each data point in a dictionary consisting of all other data points to build a similarity graph.
Segmentation of data into multiple subspaces follows by applying spectral clustering to the similarity graph.
We investigate theoretical guarantees as well as applications of SSC to problems in computer vision.
Sparse subspace clustering (SSC) is a method for clustering high-dimensional data
living in a union of low-dimensional subspaces. SSC uses the sparse representation of
each data point in a dictionary consisting of all other data points to build a similarity graph.
Segmentation of data into multiple subspaces follows by applying spectral clustering to the similarity graph.
We investigate theoretical guarantees as well as applications of SSC to problems in computer vision.
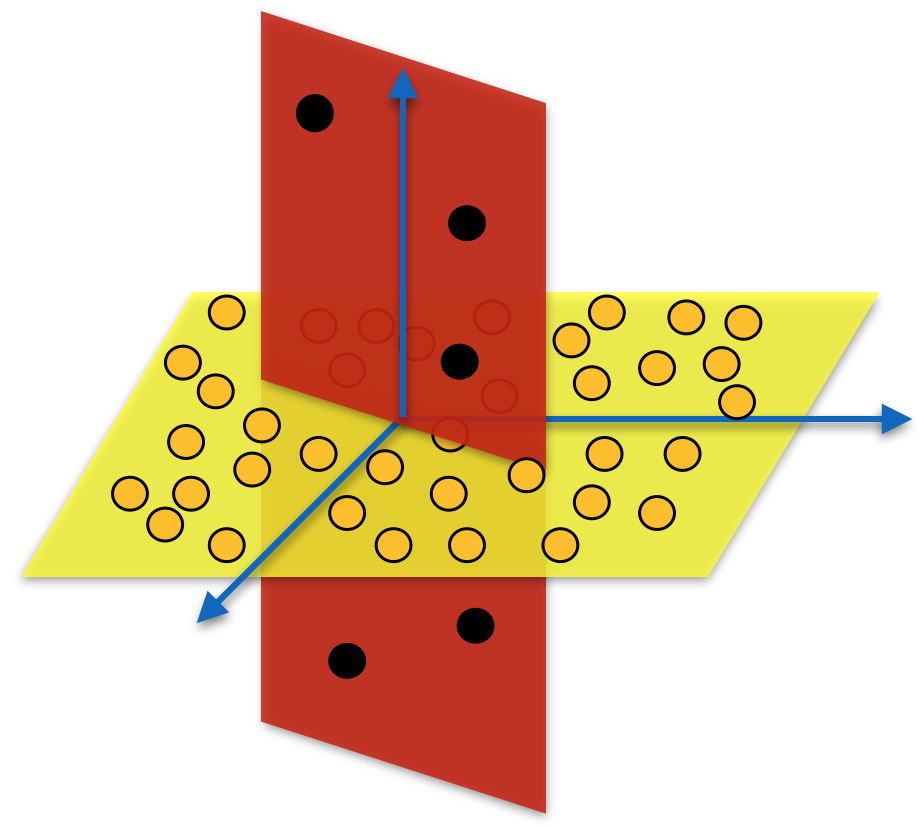
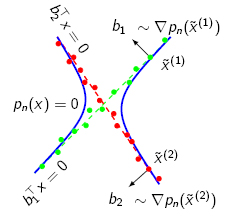 Generalized Principal Component Analysis
(GPCA) is an algebraic-geometric approach
to segmenting data lying in multiple linear subspaces. GPCA is a
non-iterative method that
operates by fitting the data with a
polynomial and then differentiating that polynomial in order to segment
the
data. This segmentation can be used to initialize iterative methods,
such as Expected Maximization.
Generalized Principal Component Analysis
(GPCA) is an algebraic-geometric approach
to segmenting data lying in multiple linear subspaces. GPCA is a
non-iterative method that
operates by fitting the data with a
polynomial and then differentiating that polynomial in order to segment
the
data. This segmentation can be used to initialize iterative methods,
such as Expected Maximization.
 Manifold
learning deals with the characterization of high dimensional data for
the goals of dimensionality reduction, classification and segmentation.
Most of nonlinear dimensionality reduction methods deal with one
manifold. We propose methods to simultaneously perform nonlinear
dimensionality reduction and clustering of multiple linear and nonlinear manifolds.
Manifold
learning deals with the characterization of high dimensional data for
the goals of dimensionality reduction, classification and segmentation.
Most of nonlinear dimensionality reduction methods deal with one
manifold. We propose methods to simultaneously perform nonlinear
dimensionality reduction and clustering of multiple linear and nonlinear manifolds.
 GEAR (Grounded Early Adaptive Rehabilitation) is a collaborative research effort between the University of Delaware and Johns Hopkins University that brings together robotics engineers,
cognitive scientists, and physical therapists, for the purpose of designing new rehabilitation environments and methods for young children with mobility disorders.
The envisioned pediatric rehabilitation environment consists of a portable harness system intended to partially compensate for body weight and facilitate the children’s mobility
within a 10 x 10 feet area, a small humanoid robot that socially interacts with subjects, trying to engage with them in games designed to make them maintain particular levels of
physical activity, and a network of cameras capturing and identifying the motion in the environment and informing the robot so that the latter adjusts its behavior depending on
that of the child. Our objective is to develop activity recognition methods that facilitate children-robot interaction.
GEAR (Grounded Early Adaptive Rehabilitation) is a collaborative research effort between the University of Delaware and Johns Hopkins University that brings together robotics engineers,
cognitive scientists, and physical therapists, for the purpose of designing new rehabilitation environments and methods for young children with mobility disorders.
The envisioned pediatric rehabilitation environment consists of a portable harness system intended to partially compensate for body weight and facilitate the children’s mobility
within a 10 x 10 feet area, a small humanoid robot that socially interacts with subjects, trying to engage with them in games designed to make them maintain particular levels of
physical activity, and a network of cameras capturing and identifying the motion in the environment and informing the robot so that the latter adjusts its behavior depending on
that of the child. Our objective is to develop activity recognition methods that facilitate children-robot interaction.
 Computerized Assessment of Motor Imitation (CAMI) is a collaborative research between Kennedy Krieger Institute, University of Washington and Johns Hopkins University that brings together neurologists, biomedical engineers, and computer scientists for the purpose of designing, developing and testing an objective, reproducible and highly-scalable multimodal system to observe children performing a brief videogame-like motor imitation task, quantitatively assess their motor imitation performance, and investigate its validity as a phenotypic biomarker for autism. Accomplishing this goal will require an interdisciplinary approach which combines expertise in autism, child development, computer vision and machine learning.
Computerized Assessment of Motor Imitation (CAMI) is a collaborative research between Kennedy Krieger Institute, University of Washington and Johns Hopkins University that brings together neurologists, biomedical engineers, and computer scientists for the purpose of designing, developing and testing an objective, reproducible and highly-scalable multimodal system to observe children performing a brief videogame-like motor imitation task, quantitatively assess their motor imitation performance, and investigate its validity as a phenotypic biomarker for autism. Accomplishing this goal will require an interdisciplinary approach which combines expertise in autism, child development, computer vision and machine learning.
 Object categorization is the task of automatically labeling objects in an image as belonging to a certain category. Segmentation involves
identifying a group of pixels as belonging to a particular object in the image. Both of these tasks are challenging problems at the core of computer vision, relevant to applications in surveillance, image search, autonomous navigation, and medical diagnostics. While existing literature treats these as separate problems, our work deals with simultaneously segmenting and categorizing objects in an image to gain more accurate results.
Object categorization is the task of automatically labeling objects in an image as belonging to a certain category. Segmentation involves
identifying a group of pixels as belonging to a particular object in the image. Both of these tasks are challenging problems at the core of computer vision, relevant to applications in surveillance, image search, autonomous navigation, and medical diagnostics. While existing literature treats these as separate problems, our work deals with simultaneously segmenting and categorizing objects in an image to gain more accurate results.
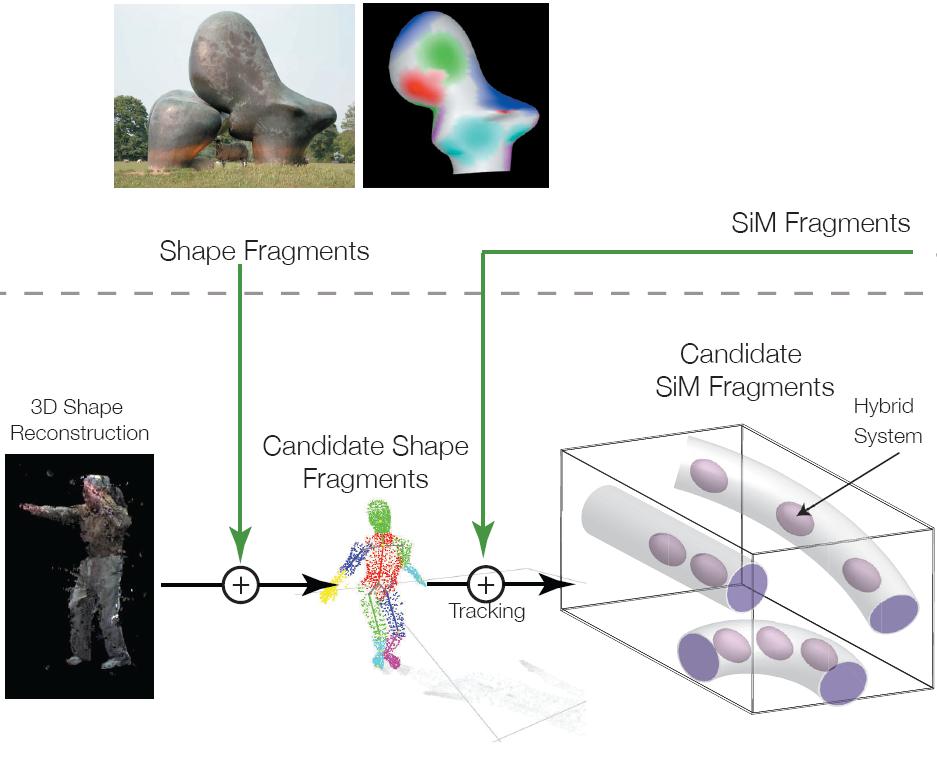 The objective of this research is to develop bio-inspired algorithms for recognizing human movements and movement styles in videos of human activities. The approach is based on a new representation of static three-dimensional (3D) shape structure in the ventral visual pathway consisting of configurations of 3D structural fragments. This project uses neural experiments to validate an analogous four-dimensional (4D) representation of moving 3D shapes based on 4D (space and time) structure-in-motion (SiM) fragments. These SiM fragment models are used to develop algorithms for automatically extracting SiM fragments from videos of human activities. Hybrid system identification and clustering techniques are used to learn a dictionary of human movements used for recognition. This dictionary, in turn, influences the design of the neural experiments. The algorithms are evaluated using a real-time tele-immersion system.
The objective of this research is to develop bio-inspired algorithms for recognizing human movements and movement styles in videos of human activities. The approach is based on a new representation of static three-dimensional (3D) shape structure in the ventral visual pathway consisting of configurations of 3D structural fragments. This project uses neural experiments to validate an analogous four-dimensional (4D) representation of moving 3D shapes based on 4D (space and time) structure-in-motion (SiM) fragments. These SiM fragment models are used to develop algorithms for automatically extracting SiM fragments from videos of human activities. Hybrid system identification and clustering techniques are used to learn a dictionary of human movements used for recognition. This dictionary, in turn, influences the design of the neural experiments. The algorithms are evaluated using a real-time tele-immersion system.
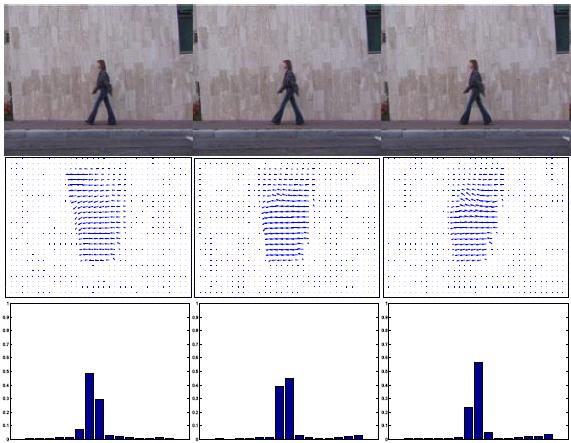 Analysis of human activities has always remained a topic of great interest in computer vision. It is seen as a stepping stone for applications such as automatic environment surveillance, assisted living and human computer interaction. There has been a tremendous amount of work in this field. Our approaches specifically model the dynamics of human activities in monocular scenes for recognition. The tools developed include representing human activities as dynamical systems, developing algorithms for efficiently learning the parameters of these representations, defining metrics on the space of these parameters and extending classification algorithms for solving the recognition problem. The general class of algorithms developed are also applicable to various other dynamic visual phenomena such as lip articulation as well as dynamic textures.
Analysis of human activities has always remained a topic of great interest in computer vision. It is seen as a stepping stone for applications such as automatic environment surveillance, assisted living and human computer interaction. There has been a tremendous amount of work in this field. Our approaches specifically model the dynamics of human activities in monocular scenes for recognition. The tools developed include representing human activities as dynamical systems, developing algorithms for efficiently learning the parameters of these representations, defining metrics on the space of these parameters and extending classification algorithms for solving the recognition problem. The general class of algorithms developed are also applicable to various other dynamic visual phenomena such as lip articulation as well as dynamic textures.
 Textures
such as grass fluttering in the wind, waves on the ocean exhibit
specific dynamics and thus can be modeled as a linear dynamical
system. The classical Brightness Constancy Constraint does not hold
good for such sequences as they are not rigid and lambertian. We
explore methods to exploit the dynamical model and achieve segmentation
and estimation of motion of a camera viewing such sequences.
Textures
such as grass fluttering in the wind, waves on the ocean exhibit
specific dynamics and thus can be modeled as a linear dynamical
system. The classical Brightness Constancy Constraint does not hold
good for such sequences as they are not rigid and lambertian. We
explore methods to exploit the dynamical model and achieve segmentation
and estimation of motion of a camera viewing such sequences.
 In this project we show how to estimate the class, 3D pose and 3D reconstruction of an object from a single 2D image. In contrast with other approaches that address these task independently, we show that there is an advantage in addressing these tasks simultaneously. In addition, we show that considering the objects in 3D is also beneficial.
In this project we show how to estimate the class, 3D pose and 3D reconstruction of an object from a single 2D image. In contrast with other approaches that address these task independently, we show that there is an advantage in addressing these tasks simultaneously. In addition, we show that considering the objects in 3D is also beneficial.
 Motion segmentation forms a quintessential
part of analyzing dynamic scenes that contain multiple rigid objects in
motion. It deals with separating visual features extracted from the
scene into different groups, such that each group has a characteristic
motion different from that of the other groups. Since we can extract a
vast bag of visual features from a scene, we explore different
approaches for segmenting the motions in the scene by using these
features.
Motion segmentation forms a quintessential
part of analyzing dynamic scenes that contain multiple rigid objects in
motion. It deals with separating visual features extracted from the
scene into different groups, such that each group has a characteristic
motion different from that of the other groups. Since we can extract a
vast bag of visual features from a scene, we explore different
approaches for segmenting the motions in the scene by using these
features.
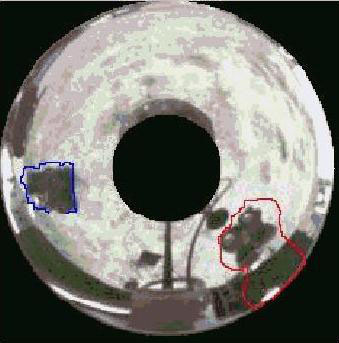 Omnidirectional motion estimating and
segmentation involves the
analysis of a scene observed from multiple central panoramic views in
order to identify the different motion patterns present in the scene.
The previous research mainly focuses on sequences captured by
perspective or affine cameras. The panoramic camera model is
mathematically more complex due to the uneven warping
in the
scene. We propose methods to estimate and segment the motion models
associated with multiple moving objects captured by panoramic cameras.
Omnidirectional motion estimating and
segmentation involves the
analysis of a scene observed from multiple central panoramic views in
order to identify the different motion patterns present in the scene.
The previous research mainly focuses on sequences captured by
perspective or affine cameras. The panoramic camera model is
mathematically more complex due to the uneven warping
in the
scene. We propose methods to estimate and segment the motion models
associated with multiple moving objects captured by panoramic cameras.
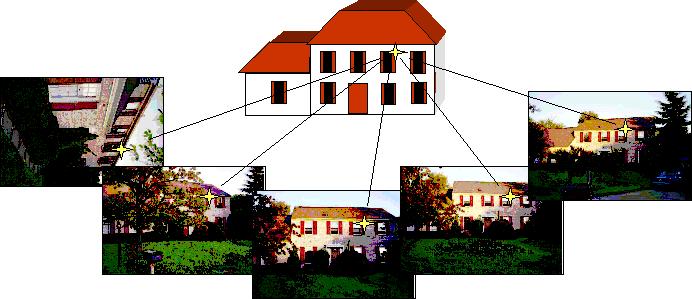 Multiple
view geometry deals with the characterization of the geometric
relationships of multiple images of points and lines. Such
characterization can be used for structure and motion recovery, feature
matching and image transfer. The previous work in multiple view
geometry is mainly restricted to a maximum of four views. We propose a
unifying geometric representation of the constraints generated by
multiple views of a scene by imposing a rank constraint on the
so-called multiple view matrix for arbitrarily
combined point
and line features across multiple views. We demonstrate that all
previously known multilinear constraints become simple instantiations
of the new condition and that quadrilinear constraints are
algebraically redundant.
Multiple
view geometry deals with the characterization of the geometric
relationships of multiple images of points and lines. Such
characterization can be used for structure and motion recovery, feature
matching and image transfer. The previous work in multiple view
geometry is mainly restricted to a maximum of four views. We propose a
unifying geometric representation of the constraints generated by
multiple views of a scene by imposing a rank constraint on the
so-called multiple view matrix for arbitrarily
combined point
and line features across multiple views. We demonstrate that all
previously known multilinear constraints become simple instantiations
of the new condition and that quadrilinear constraints are
algebraically redundant.
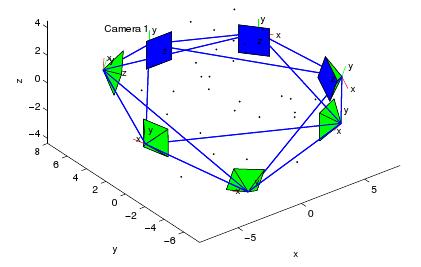
Recent hardware innovations have produced low-powered, embedded devices (also known as motes) which can be equipped with small cameras and that can communicate with neighboring units using wireless interfaces. These motes can organize themselves in a "Smart Camera Network" and represent an attractive platform for applications at the intersection of sensor networks and computer vision.
In our research we aim to find distributed solutions for Computer Vision applications. We have focused on two particular issues: distributed pose averaging and camera network localization and calibration.
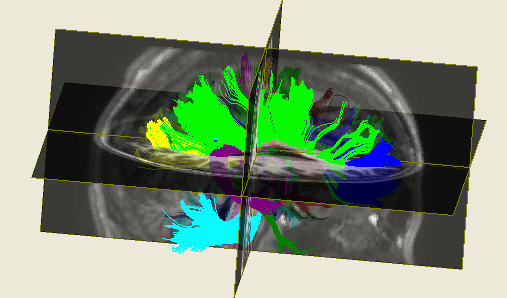
Diffusion magnetic resonance imaging (dMRI) is a medical imaging modality used to reconstruct the anatomical network of neuronal fibers in the brain, in vivo. One important goal is to use this fiber network to study anatomical biomarkers related to neurological diseases such as Alzheimer's Disease. In the Vision Lab we apply elements of Machine Learning and Computer Vision to develop computational and mathematical algorithms for dMRI reconstruction, diffusion estimation, fiber segmentation, registration, feature extraction, and disease classification.
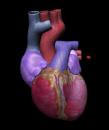 Several methods are known nowadays for treating cardiac arrhythmias -irregularities in the
heartbeat-, the least invasive of which is radiofrequency ablation. The objective of this project
is to solve the segmentation problem in order to develop a 3-D model of the heart using real time MR
images, and to help the physician during the ablation process. We use segmentation methods based on
intensity and dynamic textures framework for segmenting the heart from the chest
and the background. We then perform rigid and non-rigid registration to
register upcoming low resolution images to the previous high resolution followed by level set methods,
which integrates prior information on shape, intensity and cardiac dynamics for segmenting
different regions within the heart.
Several methods are known nowadays for treating cardiac arrhythmias -irregularities in the
heartbeat-, the least invasive of which is radiofrequency ablation. The objective of this project
is to solve the segmentation problem in order to develop a 3-D model of the heart using real time MR
images, and to help the physician during the ablation process. We use segmentation methods based on
intensity and dynamic textures framework for segmenting the heart from the chest
and the background. We then perform rigid and non-rigid registration to
register upcoming low resolution images to the previous high resolution followed by level set methods,
which integrates prior information on shape, intensity and cardiac dynamics for segmenting
different regions within the heart.
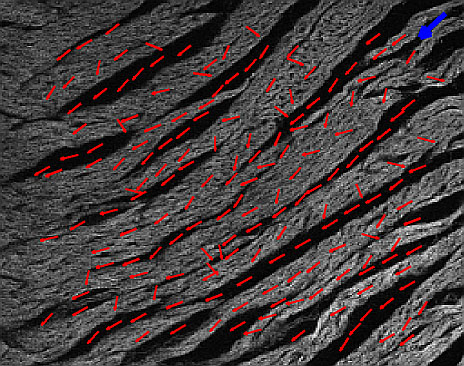 Orientation extraction and tracing of tubular structures in medical images are important
quantitative tools for developing models of the heart both at the histological and cytological
levels. The problems of detecting orientation and tracing tubular structures are closely related
to a primal problem in processing: edge detection. This has motivated several efforts in the
image processing and computer vision communities to introduce fast and robust algorithms.
However, those algorithms have to deal with not only the image noise but also the complexity
(intersection, bifurcation) of the structure. In this project, we consider the problem of extracting
spatial orientation and tracing 2-D and 3-D tubular structures in medical images. Specifically, we aim
at developing algorithms to analyze myofiber array orientation and track the 3-D Purkinje
network in cardiac data.
Orientation extraction and tracing of tubular structures in medical images are important
quantitative tools for developing models of the heart both at the histological and cytological
levels. The problems of detecting orientation and tracing tubular structures are closely related
to a primal problem in processing: edge detection. This has motivated several efforts in the
image processing and computer vision communities to introduce fast and robust algorithms.
However, those algorithms have to deal with not only the image noise but also the complexity
(intersection, bifurcation) of the structure. In this project, we consider the problem of extracting
spatial orientation and tracing 2-D and 3-D tubular structures in medical images. Specifically, we aim
at developing algorithms to analyze myofiber array orientation and track the 3-D Purkinje
network in cardiac data.
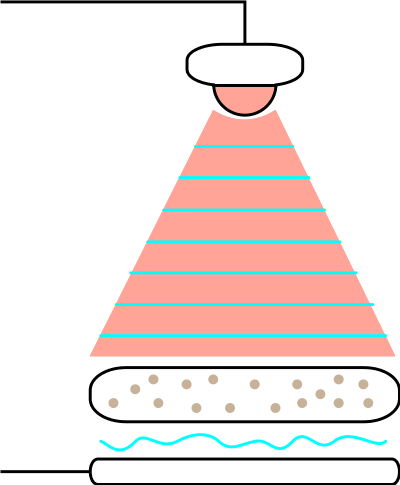 This project utilizes a microscopic imaging modality known as lens-free imaging (LFI) for a variety of biomedical applications. Lens-free imaging is based on the principle of illuminating a specimen object with a coherent light source (such as from a laser or laser diode) and then recording the resulting diffraction pattern with an image sensor. One then reconstructs an image of the object by solving an inverse model of the light diffraction process. In this project we exploit various advantages of LFI combined with computer vision techniques for a variety of biomedical point-of-care applications.
This project utilizes a microscopic imaging modality known as lens-free imaging (LFI) for a variety of biomedical applications. Lens-free imaging is based on the principle of illuminating a specimen object with a coherent light source (such as from a laser or laser diode) and then recording the resulting diffraction pattern with an image sensor. One then reconstructs an image of the object by solving an inverse model of the light diffraction process. In this project we exploit various advantages of LFI combined with computer vision techniques for a variety of biomedical point-of-care applications.