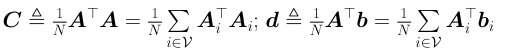JHU Computer Vision Camera Sensor Networks

Project Summary

Recent hardware innovations have produced low-powered, embedded devices (also known as motes) which can be equipped with small cameras and that can communicate with neighbouring units using wireless interfaces. Examples of these devices are the CITRIC motes and all the different types of smartphones (such as the Apple iPhone). These devices can organize themselves in a "Smart Camera Network" and represent an attractive platform for applications at the intersection of sensor networks and computer vision. In particular, flexibility is a key aspect of this technology: networks of motes or smartphones can be easily formed and expanded with the addition of new nodes on the fly.

Figure: the CITRIC mote and the iPhone

The main challenge in this setting is that each node alone has limited power and computational capabilities. Standard computer vision algorithms (e.g., Structure from Motion, target tracking, object recognition, etc.) are centralized and are not suitable for direct deployement, because they would quickly exhaust the resources of a single node. In order to perform more complex and demanding tasks, the nodes therefore need to collaborate by means of distributed algorithms. Again, standard algorithms from the Sensor Network community (e.g. averaging consensus) cannot be directly employed, due to the special structures arising in computer vision applications.

In our research we aim to extend the algorithms from the Sensor Network and Control community to find distributed solutions for Computer Vision applications, on the following several particular issues:

Distributed averaging on manifolds: we have developed algorithms that, given individual estimates of a non-Euclidean quantity (e.g., the pose of an object) at each node, consistently compute their average in a distributed fashion. Our solution differs from previous work by explicitly taking into account the intrinsic structure of the manifolds. We have applied our algorithms to the problems of distributed object averaging and face recognition.
Robust consensus in sensor networks: we have studied the problem of distributed robust optimization where the data for some nodes in the network are corrupted by outliers. Standard average consensus algorithm compute the global mean of the data as the point that minimizes the L2 norm of the distances from the measurements. We generalize this setting by considering other convex cost functions that are known to give averages that are robust to outliers, e.g., L1 norm, fair loss and Huber loss.
Consensus averaging in presence of network packet losses: standard consensus algorithms assume that, at each iteration of the algorithm, the nodes perform symmetric updates, i.e., if node i uses the data from node j, then the converse will also be true. This assumption, however, is not always verified in practice, due to packet drop during network transmissions. As a result, in real-world networks, standard consensus algorithm converge to a value which could be different from the correct average of the measuerments. We proposed a scheme where we add corrective iterations that guarantee the convergence to the correct average in spite of packet losses.
Camera network localization and calibration: when the field-of-view's of two cameras intersect, they can estimate their relative pose by using two-views epipolar geometry. We proposed algorithms that, given the noisy pose estimates between pairs of cameras, are able to consistently localize each camera in the network. Moreover, we propose algorithms that can also calibrate the internal parameters of the cameras by exploting the presence of a small number of already calibrated cameras in the network.
Applications of classical consensus algorithms to build linear distributed algorithms for computer vision and machine learning: we show how distributed averaging algorithms can be used to solve distributed linear algebraic problems, such as solving a linear system or computing the Singular Value Decomposition of a matrix. We assume that each node has access to only a subset of the problem input (e.g., a few equations of a linear system or a few row of a matrix). Using these linear algebraic solutions one can then easily build algorithms for distributed problems in computer vision and machine learning, such as Principal Component Analysis (PCA), Generalized PCA (GPCA), linear 3-D point triangulation, linear pose estimation and Affine Structure from Motion.

The algorithms illustrated in this page and other algorithms for camera sensor networks are also covered in our tutorial paper, which appeared in the IEEE Signal Processing Magazine [8].

Consensus on manifolds

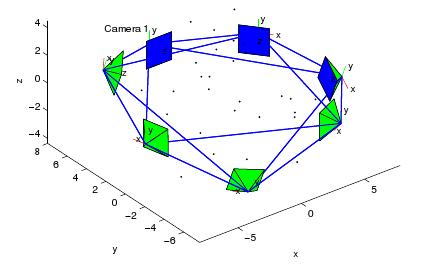
In this line of research our goal is to develop algorithms to distributely average quantities that lie on non-Euclidean manifolds. Of our particular interest is the case of pose estimation. We assume that the nodes are localized (meaning that each mote knows its position relative to its neighbours). We assume also that each node can estimate the pose of a common object (e.g. a face).

Figure: A network of cameras looking at the same object

Our goal is then to aggregate the estimates through a distributed averaging. In Sensor Networks, a popular class of algorithms for computing averages are consensus algorithms. These techniques are attractive because require communications only between neighbours and converge under mild network connectivity requirements. Unfortunately, these algorithms are designed for scalar, Euclidean quantities. On the other hand, poses are represented with a pair (R,T), where R is a rotation and T is a translation. Rotations, in particular, live on the manifold of the special orthogonal group SO(3). This means that the appropriate metric (d_m in the Figure) has to be used, instead of the Euclidean one (d_e). This induces also a new concept of average, called Karcher mean. We have developed algorithms that:

Take into account the appropriate measure of distance and the corresponding concept of Karcher mean in SO(3).

Extend consensus algorithms to average quantities in SO(3).

Show convergence to the correct average.

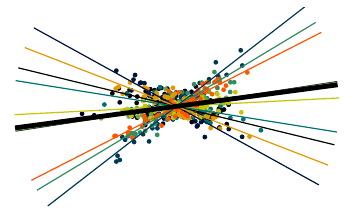
Figure: Difference between the appropriate distance in the manifold and the Euclidean distance.

Figure: Our algorithm applied to face recognition. Each camera estimate the pose of the face and communicates with the neighbors to aggregate the estimates.

Consensus with Robustness to Outliers

One of the main drawbacks of the traditional consensus algorithms is their inability to handle outliers in the measurements. This is because they are based on minimizing a Euclidean (L2) loss function, which is known to be sensitive to outliers. Thus, our objective is to propose a distributed optimization framework that can handle outliers in the measurements.
We have proposed a framework for generalization of consensus algorithms to robust loss functions that are strictly convex or convex. We pose the robust consensus problem as a constrained optimization problem, which we solve using a distributed primal-dual approach. More specifically, we try to separated the global Lagrangian function to a set of local Lagrangian functions with respect to each of the nodes in the network. We consider the problem into two classes with respect to the convexity of the cost functions.

In the case of strictly convex loss functions, the Lagrangian function is naturally distributed, hence robust consensus can be solved using local optimization at each node plus a consensus-like update of the Lagrange multipliers. The classical average consensus algorithm based on the L2 loss shows up as a special case.
In the case of non-strictly convex functions, we use an augmented Lagrangian approach that adds the square of the constraints to the cost function in order to make the problem strictly convex. However, the resulting augmented Lagrangian function is not naturally distributed. By introducing auxiliary variables and using a modified augmented Lagrangian approach, we still find a distributed solution, which involves solving a modified local optimization problem with an additional quadratic form plus the same consensus-like update of the Lagrange multipliers.

Actually our derivation is based on general functions, but as we have considered the problem of distributed robust consensus where the measurements for some nodes in the networks are corrupted by large outliers, we have applied the framework to solving the average consensus and least-squares consensus problems in a robust fashion by using the class of convex functions such that the solution of which is known to be robust to outliers, e.g., L1 loss, fair loss and Huber loss. So far, the results showed that the proposed distributed algorithm converged to the optimal solution of the equivalent centralized optimization problem for most cases.

Distributed Localization and Calibration of Camera Networks

Distributed localization of camera networks

Localization problem in a camera sensor network refers to uniquely determining the pose of every camera with respect to a fixed reference frame. More precisely, assume we have a network of n cameras deployed in 3-D. The relative pose of each camera with respect to a reference frame is defined by its rotation R and its translation T with respect to that frame. We say the network is localized if there is a set of relative transformations (R_ij,T_ij) between camera i and j such that when the reference frame for node 1 is fixed at (R₁,T₁), the other poses (R_i,T_i) are uniquely determined. When the field-of-view's of two cameras intersect, it is possible to estimate their relative transformation(R_ij,T_ij) using two-view epipolar geometry. However, there are a couple of problems in directly using these pairwise estimates.

The estimates may not be consistent if the whole network is taken into consideration. For instance, if we go trough a loop in the network, the composition of all relative transformations should give the identity.
The translations are obtained only to a scale. It is necessary to exploit the constraints from the network topology in order to find these additional scales.

Previous work either is not applicable in this setting (typically, only the case of range measurements has been considered) or does not correctly exploit the manifold structure of SE(3). In our work we developed distributed algorithm that, given the pairwise measurement, find a complete, consistent localization of the network. Moreover, our algorithm is optimal with respect to the use of the appropriate metric in SE(3).

Figure: A pictorial representation of a camera setup.

Distributed calibration of camera networks

The problem of camera calibration for a single camera has been widely studied in the computer vision literature. Such methods typically require the user to show a calibration rig to the camera. Obviously, such methods do not scale well for large camera sensor networks, because they would require manual calibration of each camera. On the other hand, self-calibration methods automatically calibrate the cameras by solving nonlinear equations such as Kruppa's equations. While these methods are very elegant, they suffer from the fact that the problem of solving Kruppa's equations is numerically ill-conditioned. Moreover, these methods assume that all the cameras have the same intrinsic parameters so they are not readily applicable to camera sensor networks, where each camera can have different intrinsic parameters. We show that the problem of automatically calibrating a large number of cameras in a sensor network can be solved in a distributed way by solving a set of linear equations. We show that this is possible under the mild assumption that only one of the cameras needs to be calibrated.
Once the cameras' intrinsic and extrinsic parameters are known, the next problem is to recover the structure of the 3D scene (triangulation problem). However, solving the multiple view triangulation problem becomes difficult in a sensor network setup. This is because, while each pair of nodes could easily compute the 3D structure of the scene via linear triangulation, the estimates from different pairs of nodes may not be the same, especially in real situations where image data are noisy. We propose a method based on distributed consensus algorithms for estimating the 3D structure of a scene in a distributed way. We show that all the nodes compute the same 3D structure, even though they communicate with only a few neighbors in the network. This method requires that all the cameras observe the same scene and that the network graph over which the nodes communicate be connected.

Applications of classical consensus algorithms to linear distributed algorithms

Many distributed algorithms for computer vision and machine learning in camera networks have been proposed in the past years. However, these algorithms often represent ad-hoc solutions for specific problems. We have devised a method which allows us to implement basic linear algebraic algorithms, such as least squares problems and SVD decomposition, through distributed averaging. Since these basic linear algebraic operations are at the core of many machine learning and computer vision applications, our techniques provide a framework that allows the straightforward extension of centralized algorithms to the distributed case. To illustrate the basic idea, consider the following problem: we would like to solve linear least squares problem

where each node has access to only some of the rows of A and b, as depicted in the figure below.

The centralized solution is given by

However, we can compute the following quantities through distributed averaging

Each node can then obtain the solution to our problem as

without any centralized coordination. Similar ideas can be used to compute the SVD of the matrix A and to estimate its nullspace. These basic algorithms can then be applied to different problems.

Affine Subspace Fitting. Imagine that each node collects a set of vectorial measurements. We would like to fit an affine subspace to the dataset constituted by the union of the measurements from all the nodes.

Figure: a representation of the distributed PCA problem. Different colors represent data (points) and locally estimated subspaces (thin lines) for different nodes. The thick black line represents the global solution estimated by the algorithm.

In a centralized setting, one can use PCA, which is implemented by centering the data around its mean and computing an SVD. Following the ideas highlited before, both these operations can be implemented through distributed averaging.
Subspace segmentation. Similarly to the affine subspace fitting problem above, assume that each node collects a set of vectorial measurements. However, here we assume that they have been generated from a union of subspaces, and we are interested in learning these subspaces and segment the data. Generalized PCA (GPCA) is a technique that models the union of subspaces as the zero-set of a multivariate polynomial. The coefficients of this polynomial can be obtained by estimating the nullspace of the matrix formed by the Veronese map of the data. This operation can be performed through distributed averaging and the subspaces can obtained from the coefficients of the polynomial using simple distributed minimum operations.
Point triangulation and linear pose estimation. Assume that a set of cameras, with known poses, can detect the image coordinates of a common set of 3-D points. If the location of the 3-D points is unknown, standard computer vision techniques provide a way to obtain two linear constraints on the location of the point from each 2-D image. If we consider all these constraints together, we have a distributed least squares problem that can be solved through distributed averaging. Similarly, if the 3-D points corresponds to a known 3-D object under an unknown pose, one can obtain, a set of linear contraints on the rotation matrix and the translation vector of the pose from each camera. These quantities can then be estimated by solving the obtained distributed least squares problem.
Affine Structure from Motion. Assume that we have a set of cameras tracking a moving object in the scene. If we assume the affine projection model for the cameras, one can reconstruct the 3-D structure and obtain the relative pose between each camera and the moving object by using Affine Structure from Motion techniques.

Figure: two cameras tracking a common 3-D moving object.

In a centralized case, the poses and the 3-D structure can be obtained by creating a matrix with the images of the tracked points, factorizing it and then solving a linear system to bring the factorization in a canonical form. All these steps can be implemented following our framework using distributed averaging.